How to Cite
Copyright notice
Authors who publish with this journal agree to the following terms:
Authors retain copyright and grant the journal right of first publication, with the work twelve (12) months after publication simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work’s authorship and initial publication in this journal.
- After 12 months from the date of publication, authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
Keywords
Abstract
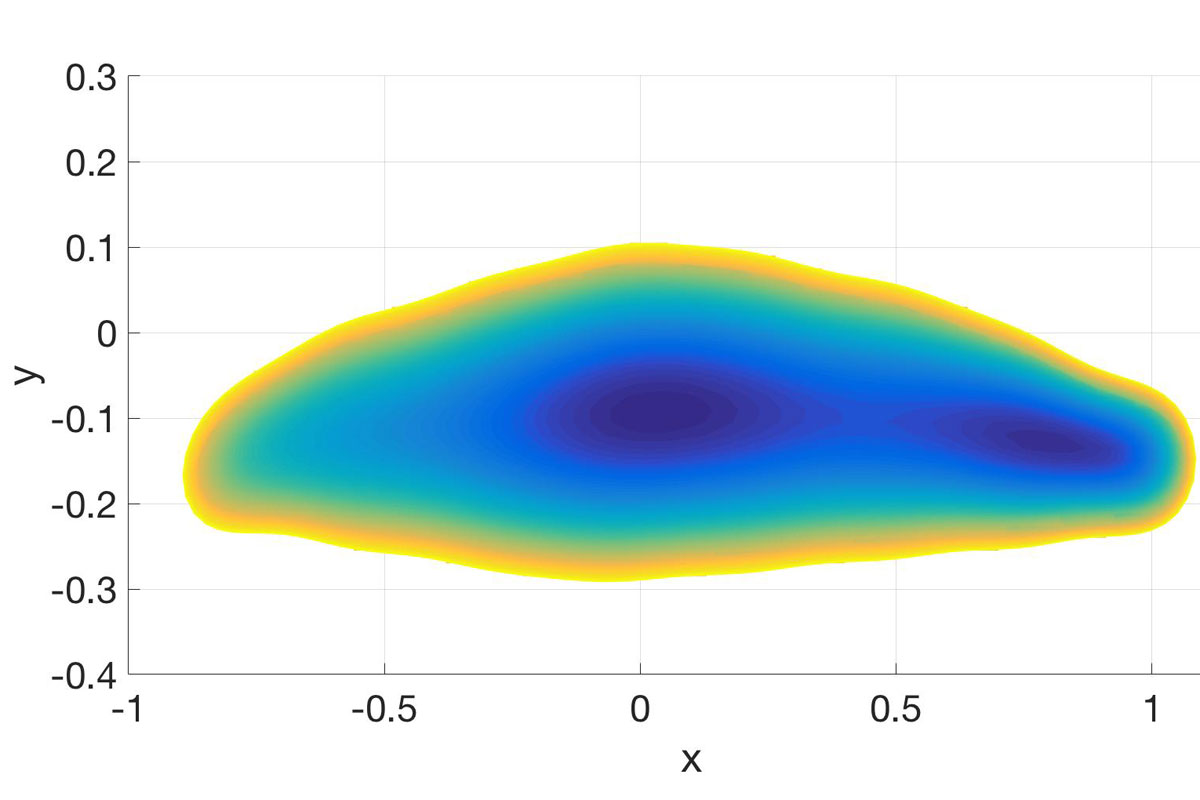
Each time one blinks, a stable tear film (TF) must reestablish itself on the ocular surface to ensure the function and health of the eye. Although the formation of the TF has been extensively studied both experimentally and theoretically, the influence of the lid dynamics on the TF formation is still not fully understood. Experimental instrumentation does not yet have the capability to estimate the TF thickness in vivo over the entire front of the eye, especially near the lids during a blink, where the eyelashes obstruct the view of the ocular surface. Additionally, a realistic blinking eyeshaped domain presents challenges in approximating themotion of the TF in theoretical studies. In thiswork,we overcome these theoretical challenges by implementing a moving overset grid method to study the influence of the lid motion on the formation of TF.
References
Braun R, King-Smith P, Begley C, Li L, Gewecke N. Dynamics and function of the tear film in relation to the blink cycle. Prog Ret Eye Res. 2015;45: 132-164.
Braun RJ. Dynamics of the tear film. Annu Rev Fluid Mech. 2012;44:267–297.
King-Smith E, Fink B, Hill R, Koelling K, Tiany J. The thickness of the tear film. Curr Eye Res. 2004;29(4-5):357-368.
Maki KL, Braun RJ, Ucciferro P, Henshaw WD, King-Smith PE. Tear film dynamics on an eye-shaped domain. Part 2. Flux boundary conditions. J Fluid Mech. 2010;647:361–390.
Heryudono A, Braun RJ, Driscoll TA, Cook LP, Maki KL, King-Smith PE. Single-equation models for the tear film in a blink cycle: Realistic lid motion. Math Med Biol. 2007;24:347–377.
Maki KL, Braun RJ, Driscoll TA, King-Smith PE. An overset grid method for the study of reflex tearing. Math Med Biol. 2008;25: 187–214.
Mainstone JC, Bruce AS, Golding TR. Tear meniscus measurement in the diagnosis of dry eye. Curr Eye Res. 1996;15(6):653–661.
Golding TR, Bruce AS, Mainstone JC. Relationship between tear-meniscus parameters and tear-film breakup. Cornea. 1997;16(6):649–661.
Gaffney E, Tiffany J, Yokoi N, Bron A. A mass and solute balance model for tear volume and osmolarity in the normal and the dry eye. Prog Ret Eye Res. 2010;29(1):59 –78.
Doane MG. Blinkingand the mechanics of the lacrimal drainage system. Ophthalmology. 1981;88: 844–851.
Jones MB, Please CP, McElwain DLS, Fulford GR, Roberts AP, Collins MJ. Dynamics of tear film deposition and drainage. Math Med Biol. 2005;22:265–288.
Mishima S, Gasset A, Klyce SD, Baum JL. Determination of tear volume and tear flow. Ophthalmol Vis Sci. 1966;5:264–276.
Chesshire G, Henshaw WD. Composite overlapping meshes for the solution of partial differential equations. J Comput Phys. 1990;90:1–64.
Henshaw WD, Schwendeman DW. Moving overlapping grids with adaptive mesh refinement for high-speed reactive and non-reactive flow. J Comput Phys. 2006;216(2):744 –779.
Roache PJ. Verification of codes and calculations. AIAA J. 1998;36(5): 696–702.
Li L, Braun RJ, Maki KL, Henshaw WD, King-Smith PE. Tear film dynamics with evaporation, wetting and time-dependent flux boundary condition on an eye-shaped domain. Phys Fluids. 2014;26:052101.